Nouveau système de calcul du classement Elo

Texte officiel de l’ICCF traduit par Jean-François Épinoux.

Guide du débutant sur le système de classement ICCF révisé

Mark Glickman, Département des statistiques, Université de Harvard

À partir de 2023, l’ICCF adoptera un nouveau système de classement pour évaluer les résultats des parties jouées lors des événements de l’ICCF. La décision de réviser le système de classement est le résultat d’une prise de conscience que l’ancien système n’était plus en mesure de calculer des classements exacts. Cela était particulièrement évident aux plus hauts niveaux de jeu, où la fréquence des parties nulles avait augmenté à un point tel que les classements des joueurs les mieux classés ne changeaient pratiquement pas.

En 2021, les délégués de l’ICCF ont reconnu la nécessité d’un nouveau système qui répondrait au problème de l’augmentation de la fréquence des parties nulles. À cette fin, ils ont demandé au Dr Mark Glickman, expert respecté en matière de systèmes de classement et maître de conférences à l’université de Harvard, de mettre au point un système sur mesure. M. Glickman est bien connu pour son travail sur les systèmes de classement Glicko et Glicko-2, qui ont été mis en œuvre dans diverses organisations d’échecs telles que chess.com et lichess.org. Il a également été l’un des co-développeurs du système de classement universel utilisé par le Grand Chess Tour.

Le Dr Glickman a développé le système ICCF révisé d’août 2021 à mai 2022, en utilisant plus de six ans de résultats de parties ICCF et d’informations sur les classements actuels pour affiner les formules. Les détails du nouveau système ont été présentés aux délégués de l’ICCF en juin 2022 et ont été acceptés en août 2022. La mise en œuvre des formules à l’usage de l’ICCF a commencé peu après.

Ce document décrit les caractéristiques de base du nouveau système d’évaluation et s’adresse à un public non technique.

Notations et écarts de notation :

L’un des changements significatifs par rapport à l’ancien système de classement est l’ajout d’un écart de classement (abrégé RD) pour chaque joueur. Il s’agit d’un concept emprunté au système de classement de Glicko1 développé il y a environ 30 ans. Le classement, comme dans l’ancien système de l’ICCF, est une mesure de la force de jeu d’un joueur. Le RD est une mesure du manque de fiabilité du classement. Plus le RD d’un joueur est élevé, moins son classement est fiable. Un RD d’environ 75 ou moins indique que l’évaluation d’un joueur est fiable et digne de confiance.

Les joueurs qui ne sont pas classés (en supposant qu’il n’y ait pas d’autre classement externe, tel qu’un classement FIDE) commencent avec un classement de 1800 et un RD de 250, le plus grand RD possible dans le nouveau système. Cette attribution signifie que notre meilleure estimation de la cote du joueur, sans aucune information supplémentaire, est 1800. Cependant, le RD de 250 indique que la cote de 1800 est très incertaine. Pour les joueurs de la FIDE qui ne sont pas classés par l’ICCF, le RD de départ est fixé à 150. Généralement, les joueurs qui ont des RD élevés sont soit des joueurs provisoires, soit des joueurs qui n’ont pas participé à des compétitions récemment et dont les classements sont périmés. À l’inverse, les joueurs dont le classement est établi et qui participent fréquemment à des compétitions ont tendance à avoir des RD faibles. L’inclusion des RD dans le système de classement révisé de l’ICCF a des implications importantes pour les jeux de classement. Les RD peuvent influer sur l’évolution du classement d’un joueur en fonction des résultats de la partie et sur l’évolution du classement de son adversaire.

Par exemple, supposons que deux joueurs, Sarah et Joe, ayant le même classement, jouent une partie et que Sarah gagne. Si les deux joueurs ont des RD faibles, ce qui signifie que leurs classements reflètent de manière fiable leur force de jeu, le nouveau système de classement ne modifiera probablement pas beaucoup le classement de Sarah et de Joe, car leurs classements étaient déjà fiables avant qu’ils ne jouent. En revanche, si le DR de Sarah est faible et que celui de Joe est élevé, ce qui indique que son classement n’est pas fiable, le classement de Sarah augmentera à peine, car elle a battu un adversaire dont le classement n’est pas fiable. En revanche, la note de Joe devrait diminuer de manière significative, car il a perdu contre un adversaire dont la note est précise, et sa propre note n’était pas fiable au départ. Enfin, si la note de Sarah est élevée et celle de Joe faible, la note de Sarah augmentera considérablement, car sa note n’est pas fiable et celle de Joe est précise.

En général, lorsque le RD d’un joueur est élevé, on peut s’attendre à ce que les changements d’évaluation soient plus importants. Inversement, lorsque le RD d’un joueur est faible, ses changements de notation ont tendance à être plus faibles. En outre, lorsqu’un joueur affronte un adversaire dont le RD est élevé, le résultat du match n’a généralement que peu d’impact sur sa propre cote. En revanche, lorsqu’il s’agit d’affronter un adversaire dont le RD est faible, le résultat du jeu peut entraîner des changements plus importants dans le classement du joueur.

Le système de classement ICCF révisé a été conçu pour permettre aux joueurs ayant un DR élevé d’améliorer leur classement plus rapidement qu’auparavant. Parce que les joueurs avec des RD élevés ont tendance à recevoir des augmentations de classement plus importantes (en termes absolus) que ceux avec des RD faibles, un joueur avec un RD élevé peut jouer plusieurs parties et améliorer rapidement son classement dans un laps de temps relativement court. Cette approche vise à inciter les joueurs qui participent pour la première fois aux événements de l’ICCF à commencer à jouer des parties cotées, et à récompenser les joueurs provisoires qui participent régulièrement à un plus grand nombre de parties cotées.

Procédure d’évaluation :

Le système de classement ICCF révisé met à jour les classements des joueurs et les RD tous les trois mois, tout comme l’ancien système. Voici les étapes du processus de classement, qui se répète tous les trimestres :

1. Déterminer le classement et le RD de chaque joueur au début de la période de classement de trois mois.

2. Mettre à jour le classement et le RD de chaque joueur en utilisant les nouvelles formules de classement, sur la base des matchs disputés au cours de la période de trois mois. Cette étape entraînera une diminution du RD pour chaque joueur.

3. Utiliser les formules pour augmenter le RD de chaque joueur en raison du passage du temps afin de produire un nouveau RD qui sera utilisé au début de la période de 3 mois suivante.

Quelques commentaires méritent d’être formulés pour expliquer ce processus. Tout d’abord, au début de chaque période de classement, chaque joueur se voit attribuer un classement et un RD, même s’il n’est pas classé. Les joueurs non classés se voient attribuer un classement et un DR (généralement une valeur élevée) qui ne sont pas basés sur les résultats des matchs de l’ICCF. Ils peuvent être basés sur des informations de classement connues provenant d’un autre système de classement (par exemple, la FIDE), ou comme mentionné ci-dessus, ils se verront attribuer un classement de 1800 et un RD de 250 si aucune autre information n’est disponible.

Deuxièmement, tous les résultats des matchs au cours d’une période de trois mois sont évalués simultanément. Cela signifie que le classement et le RD de chaque joueur sont mis à jour simultanément sur la base de tous les matchs réalisés au cours de la période de classement. Alors que le classement d’un joueur peut augmenter ou diminuer, le RD basé sur l’étape 2 diminue toujours. Ceci reflète l’idée que plus les résultats des matchs sont enregistrés, plus le classement actualisé du joueur devient une mesure fiable de sa force de jeu.

Enfin, il est important de noter qu’après la diminution du RD due aux résultats des matchs à l’étape 2, le RD est ensuite augmenté à l’étape 3 pour tenir compte du passage du temps, et cette nouvelle valeur est utilisée au début de la prochaine période de classement de 3 mois. Même si un joueur ne termine aucun match au cours de la période, son RD augmentera quand même. En effet, plus le temps passe, plus il y a d’incertitude sur les capacités d’un joueur – il peut être en train d’améliorer activement son jeu ou se rouiller en négligeant le jeu d’échecs. L’augmentation de la RD reflète l’idée que nous sommes légèrement moins sûrs de la force du joueur après plusieurs mois. Toutefois, il convient de noter que les RD supérieurs à 120 n’augmentent pas avec le temps ; ils ne peuvent augmenter que lorsque les RD tombent en dessous de 120.

Probabilités distinctes pour les victoires, les défaites et les nuls :

L’une des principales motivations de la révision du système de classement de l’ICCF était la fréquence nettement plus élevée des parties nulles chez les joueurs les mieux classés par rapport aux joueurs les moins bien classés. Cela s’est traduit par des changements de classement généralement moins importants pour les joueurs de haut niveau qui ont rarement des parties décisives contre des adversaires de force similaire. L’une des limites du système précédent était qu’il était basé sur les formules d’Arpad Elo des années 1950, qui ne tenaient pas compte de la probabilité d’un match nul en fonction des niveaux de compétence des joueurs. Le système s’appuyait uniquement sur une formule pour déterminer le résultat attendu ou l’espérance de gain d’un match, qui reposait uniquement sur la différence de classement entre deux joueurs. Par conséquent, le système n’était pas en mesure de résoudre le problème de la fréquence élevée des parties nulles parmi les joueurs les mieux classés.

Le système de classement ICCF révisé comprend trois probabilités distinctes pour chaque type de résultat (victoire, défaite ou match nul), au lieu d’une seule espérance de gain basée uniquement sur la différence de classement entre les deux joueurs concernés. Les probabilités de chaque résultat sont calculées en fonction des classements et des RD des joueurs. Plus les deux classements sont proches l’un de l’autre, plus la probabilité d’un match nul est élevée. De même, plus les RD de deux joueurs sont élevés, ce qui indique le manque de fiabilité des évaluations des joueurs, plus la probabilité d’un match nul est élevée. En outre, le système révisé reconnaît que les joueurs bien classés ont tendance à faire match nul les uns contre les autres à un taux plus élevé que les joueurs moins bien classés. Une conséquence de cette reconnaissance est que les gains et les pertes de classement basés sur les parties décisives peuvent être plus prononcés. Par exemple, un joueur classé 1500 qui bat un joueur classé 1300 gagne 20 points (en supposant que les deux joueurs ont un RD de 100), tandis qu’un joueur classé 2500 qui bat un joueur classé 2300 voit son classement augmenter de 24 points, soit plus que le gain de classement de la paire de joueurs moins bien classés.

Les formules permettant de calculer les probabilités d’issue de chaque partie et les formules permettant de modifier les classements en fonction de ces probabilités ont été élaborées à partir de l’analyse de plus de six années de résultats de parties précédentes de l’ICCF. L’optimisation du système de classement dans le seul but de produire des probabilités exactes entraînerait des changements de classement trop importants, et les classements des meilleurs joueurs ne changeraient pratiquement pas en fonction des parties nulles. Au lieu de cela, la dérivation des formules a été un compromis entre trois facteurs : (1) produire des calculs de probabilité précis des résultats des parties, (2) éviter l’inflation des classements, et (3) maintenir la distribution des classements dans le temps. Alors que le taux de parties nulles parmi les meilleurs joueurs de ces dernières années est largement supérieur à 95 %, les formules finales calculent des probabilités de l’ordre de 80 %. Cette légère imprécision permet un plus grand mouvement des cotes aux niveaux les plus élevés et empêche les dérives involontaires de la moyenne de toutes les cotes.

Les graphiques ci-dessous illustrent les probabilités de victoire, de match nul et de défaite pour un joueur ayant un classement et un RD donnés, ainsi que le changement de classement correspondant pour chaque résultat de match.

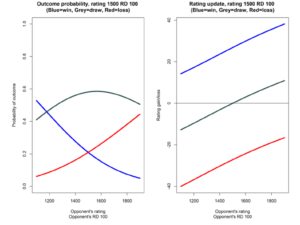
Légendes de gauche à droite et de haut en bas :

• Probabilité de réalisation, taux 2500 RD 100

(Bleu=gagnant, Gris=nul, Rouge=perdant)

• Classement de l’adversaire

RD de l’adversaire 100

La figure ci-dessus correspond à un joueur ayant un classement de 1500 et un RD de 100. Le graphique de gauche montre les probabilités de victoire (courbe bleue), de match nul (courbe grise) et de défaite (courbe rouge) contre un adversaire dont le classement est indiqué sur l’axe horizontal (et dont le RD est de 100). Par exemple, lors d’une compétition contre un adversaire ayant une cote de 1400 et un RD de 100, la probabilité de perdre contre cet adversaire est d’environ 0,16, la probabilité de faire match nul est d’environ 0,565 et la probabilité de gagner est d’environ 0,28. La probabilité d’un match nul est la plus élevée (point le plus haut sur la courbe grise du graphique de gauche) lorsque la cote de l’adversaire est également de 1500. Il convient de noter que la probabilité d’un match nul contre un adversaire classé 1900 (400 points de plus que le joueur classé 1500) est un peu plus élevée que la probabilité d’un match nul contre un adversaire classé 1100 (400 points de moins que le joueur classé 1500), comme on peut le voir en comparant la hauteur de la courbe grise à droite et à gauche du graphique. Cela s’explique par le fait que le système de classement révisé reconnaît que les paires de joueurs mieux classés ont tendance à faire plus souvent match nul que les paires de joueurs moins bien classés. Dans ce cas, la probabilité d’un match nul entre des joueurs classés 1500 et 1900 est plus élevée que la probabilité d’un match nul entre des joueurs classés 1500 et 1100 parce que le premier ensemble de classements est, en moyenne, plus élevé que le second.

Le graphique de droite montre l’évolution de la cote en cas de victoire (bleu), de match nul (gris) et de défaite (rouge) contre un adversaire dont la cote est indiquée sur l’axe horizontal. Si la cote de l’adversaire est de 1500 (et son RD de 100), la cote du joueur ne change pas si le résultat est un match nul, mais le gain de cote est d’environ 27 points pour une victoire, et une baisse de 27 points pour une défaite. Une fois encore, il convient de noter l’asymétrie du changement de classement lorsque l’on joue contre un adversaire dont le classement est supérieur de 400 points à celui d’un adversaire dont le classement est inférieur de 400 points. Par exemple, lorsqu’il tire un adversaire dont le classement est supérieur de 400 points, le joueur de 1500 points gagne 11 points. En revanche, lorsqu’il affronte un adversaire dont la cote est inférieure de 400 points, il perd 13 points. Cette asymétrie reflète le fait qu’il est plus probable de tirer un adversaire mieux classé que de tirer un adversaire moins bien classé, car les chances d’un résultat décisif sont plus élevées.

La même analyse peut être illustrée pour un joueur ayant une cote de 2500 et un RD de 100

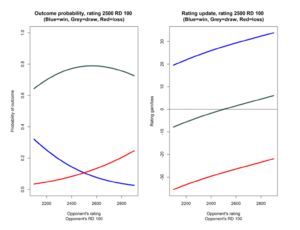
Légendes de gauche à droite et de haut en bas :

• Probabilité de réalisation, taux 2500 RD 100

(Bleu=gagnant, Gris=nul, Rouge=perdant)

• Classement de l’adversaire

RD de l’adversaire 100

Il y a plusieurs différences à souligner par rapport à l’analyse du joueur classé 1500. D’après le graphique de gauche, la probabilité d’un match nul est largement supérieure à 0,6 lorsqu’un joueur classé à 2500 joue contre un adversaire dont la cote se situe entre 2100 et 2900 (et dont le RD est de 100), avec un pic d’environ 0,8 lorsque la cote de l’adversaire est également de 2500. Cette probabilité est bien plus élevée que la probabilité de match nul d’un joueur classé à 1500 contre un adversaire situé à moins de 400 points de classement. Le graphique de droite, qui montre l’évolution de la cote à la suite d’une victoire, d’un match nul ou d’une défaite, présente quelques caractéristiques importantes qui méritent d’être soulignées. Alors que l’augmentation de la cote pour une victoire contre un adversaire ayant la même cote est à peu près la même (27 points pour les joueurs classés à 1500 et 28 points pour les joueurs classés à 2500), l’augmentation de la cote pour une victoire d’un joueur classé à 2500 ne dépend pas autant de la cote de l’adversaire que pour un joueur classé à 1500. En d’autres termes, un joueur de 2500 points battant un adversaire classé 200 points plus bas (avec un RD de 100) obtient une augmentation de 24 points, alors qu’un joueur de 1500 points battant un adversaire classé 200 points plus bas n’obtiendrait qu’une augmentation de 20 points. Les courbes du graphique de droite pour le joueur de 2500 points sont plus “plates” que les courbes du graphique de droite pour le joueur de 1500 points. Cela signifie que, pour les joueurs les mieux classés, les résultats décisifs des matchs peuvent entraîner des changements de classement plus importants.

Synthèse :

Le système de classement révisé reconnaît que les paires de joueurs mieux classés ont tendance à faire des matchs nuls plus fréquemment que les paires de joueurs moins bien classés, ce qui entraîne des changements de classement un peu plus importants pour les résultats de matchs décisifs pour les joueurs mieux classés. De plus, l’incorporation d’un RD comme mesure de la non-fiabilité du classement profite aux joueurs de tous les classements, ce qui se traduit par des classements plus précis qui reflètent mieux le niveau de compétence d’un joueur.

Pour passer au nouveau système de classement, l’ICCF utilisera les classements existants d’il y a plusieurs années comme point de départ. Lorsque le nouveau système sera mis en place, le RD d’un joueur sera initié sur la base du nombre de parties récemment jouées. Plus de détails sur la mise en place du nouveau système sont à venir.

Les joueurs qui souhaitent en savoir plus sur les détails techniques de l’algorithme de classement révisé sont invités à lire les spécifications techniques à l’adresse [insérer le lien ici]. Une calculatrice en ligne qui met en œuvre les nouvelles formules de classement est disponible à l’adresse https://ratingscalculator.azurewebsites.net/, permettant aux joueurs de calculer leurs propres changements de classement.

L’AJEC remercie Jean-Marc Épinoux pour la traduction du texte publié en anglais sur le site de l’ICCF